data-structures-and-algorithms
Обход графа в ширину
Существует два основных алгоритма обхода графов. Рассмотрим один из них.
Breadth First Search (BFS) - это алгоритм последовательного обхода вершин графа по уровням k, то есть перед тем как приступить к поиску вершин на расстоянии k+1 от заданной вершины, выполняется обход всех вершин на расстоянии k. Метод не учитывает иерархию структуры данных, а лишь глубину уровней. Одним из наиболее частых случаев применения BFS можно назвать поиск кратчайшего расстояния от заданной вершины до искомой.
Для обхода графа в ширину используется несколько техник, например с использованием очереди или метод сохранения вершин. Рассмотрим более детально алгоритм с использованием очереди. Дан граф G(V, E), требуется обойти все его вершины V.
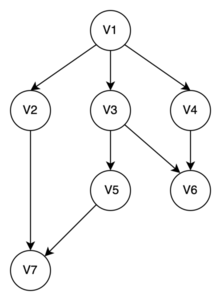
Цветовая гамма: зеленый — вершина в обработке, серый — вершина найдена, но ждет своей обработки, красный — вершина исключена из очереди.
-
Кладем заданную вершину V1 в очередь Q.

-
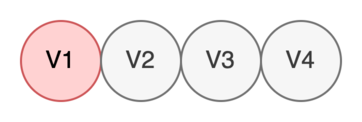
Находим все дочерние вершины V1: V2, V3, V4. Кладем найденные вершины в очередь и помечаем V1 как обработанную, т.е. исключаем ее из очереди.
-
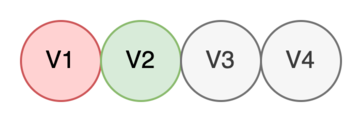
Берем в работу V2.
-
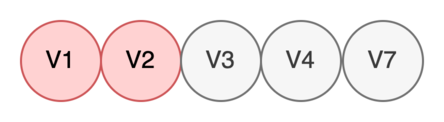
Находим все дочерние вершины V2: V7. Кладем найденные вершины в очередь и помечаем V2 как обработанную.
-
Берем в работу V3.
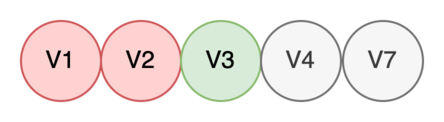
-
Находим все дочерние вершины V3: V5, V6. Кладем найденные вершины в очередь и помечаем V3 как обработанную.
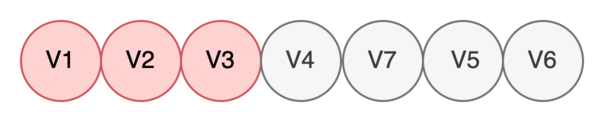
-
Берем в работу V4.
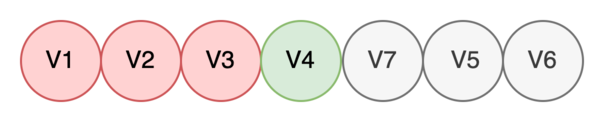
-
Находим все дочерние вершины V4: V6. Видим, что найденная вершина V6 уже определена, поэтому просто помечаем V4 как обработанную.
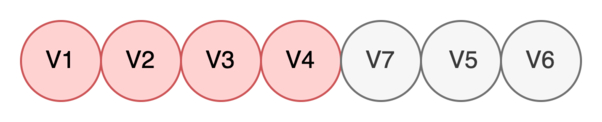
-
Берем в работу V7.
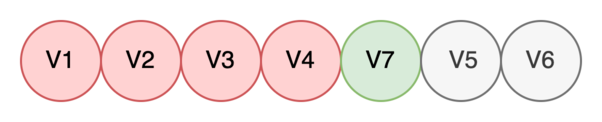
-
Дочерних вершин у нее нет, поэтому в очередь класть нечего. Сразу помечаем V7 как обработанную.
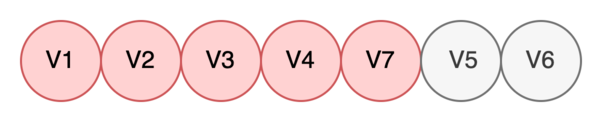
-
Берем в работу V5.
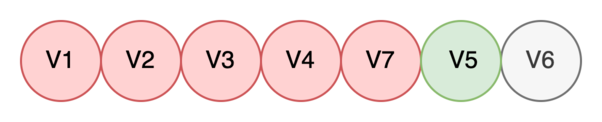
-
Находим все дочерние вершины V5: V7. Видим, что найденная вершина V7 уже определена, поэтому просто помечаем V5 как обработанную.
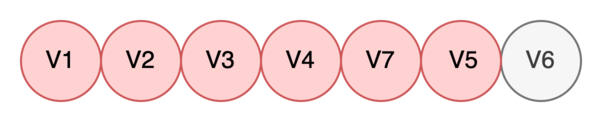
-
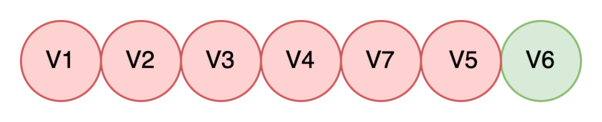
Берем в работу V6. Дочерних вершин у нее нет, поэтому в очередь класть нечего. Сразу помечаем V6 как обработанную.
-
Видим, что очередь пустая, поэтому больше брать в работу нечего. Мы обошли весь граф. Завершаем алгоритм.
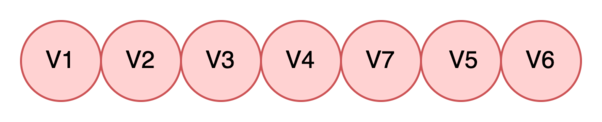
Теперь, изучив алгоритм боле детально, напишем его реализацию на python. Здесь класс Node описывает вершину графа,
функция bfs производит обход графа в ширину, а функция bfs_2 является модификацией bfs. В процессе ее работы
мы не посещаем уже обработанные вершины.
from collections import deque
from typing import Optional, List, Tuple, Hashable
class Node:
def __init__(self, data: int, children: Optional[List['Node']] = None):
self.data = data
self.children = children
def __repr__(self):
return str(self.data)
def __hash__(self):
return hash(self.data)
def __eq__(self, other):
return self.data == other.data
def test_bfs():
graph = Node(1, [
Node(2, [Node(7)]),
Node(3, [
Node(5, [Node(7)]),
Node(6),
]),
Node(4, [Node(6)]),
])
print('\n')
print(isinstance(Node(6), Hashable))
print(hash(Node(6)))
step, node = bfs_2(graph, 6)
assert 2 == step
assert node.data == 6
step, node = bfs_2(graph, 7)
assert 2 == step
assert node.data == 7
def bfs(root: Node, target: int) -> Tuple[int, Optional[Node]]:
"""
Обход графа в ширину с поиском значения атрибута Node.data
:param root: Начальная вершина графа.
:param target: искомое значение
:return: (step, node) - кратчайший путь между вершинами, найденная вершина. Если не найдено, None
"""
queue = deque() # хранение всех вершин, которые ожидают обработки
step = 0 # количество необходимых шагов, чтобы достичь искомую вершину
# инициализация
queue.append(root)
while len(queue) > 0: # пока очередь не пуста
print(f'============== Step: {step} ==============')
size = len(queue)
# обработка элементов, которые находятся в очереди, те вершин одного уровня
for _ in range(size):
current_node = queue.popleft()
print(f'Node: {current_node}')
if current_node.data == target:
return step, current_node
if current_node.children:
for child in current_node.children:
queue.append(child)
step += 1
return step, None # вершина не найдена
def bfs_2(root: Node, target: int) -> Tuple[int, Optional[Node]]:
"""
Обход графа в ширину без посещения уже обработанных вершин с поиском значения атрибута Node.data
:param root: Начальная вершина графа.
:param target: искомое значение
:return: (step, node) - кратчайший путь между вершинами, найденная вершина. Если не найдено, None
"""
queue = deque() # хранение всех вершин, которые ожидают обработки
visited = set() # вершины, которые уже посетили
step = 0 # количество необходимых шагов, чтобы достичь искомую вершину
# инициализация
queue.append(root)
visited.add(root)
while len(queue) > 0: # пока очередь не пуста
print(f'============== Step: {step} ==============')
size = len(queue)
# обработка элементов, которые находятся в очереди, те вершин одного уровня
for _ in range(size):
current_node = queue.popleft()
print(f'Node: {current_node}')
if current_node.data == target:
return step, current_node
if current_node.children:
for child in current_node.children:
if child not in visited:
queue.append(child)
visited.add(child)
step += 1
return step, None # вершина не найдена
Пространственная сложность
Так как в памяти хранятся все развёрнутые узлы, пространственная сложность алгоритма составляет O(V+E).
Временная сложность
Так как в худшем случае алгоритм посещает все узлы графа, временная сложность алгоритма составляет O(V+E).