data-structures-and-algorithms
Двусвязный список
В то время как объекты односвязного списка хранят ссылки только на следующие элементы, в двусвязном списке присутствуют обе связи на следующий и предыдущий элемент.
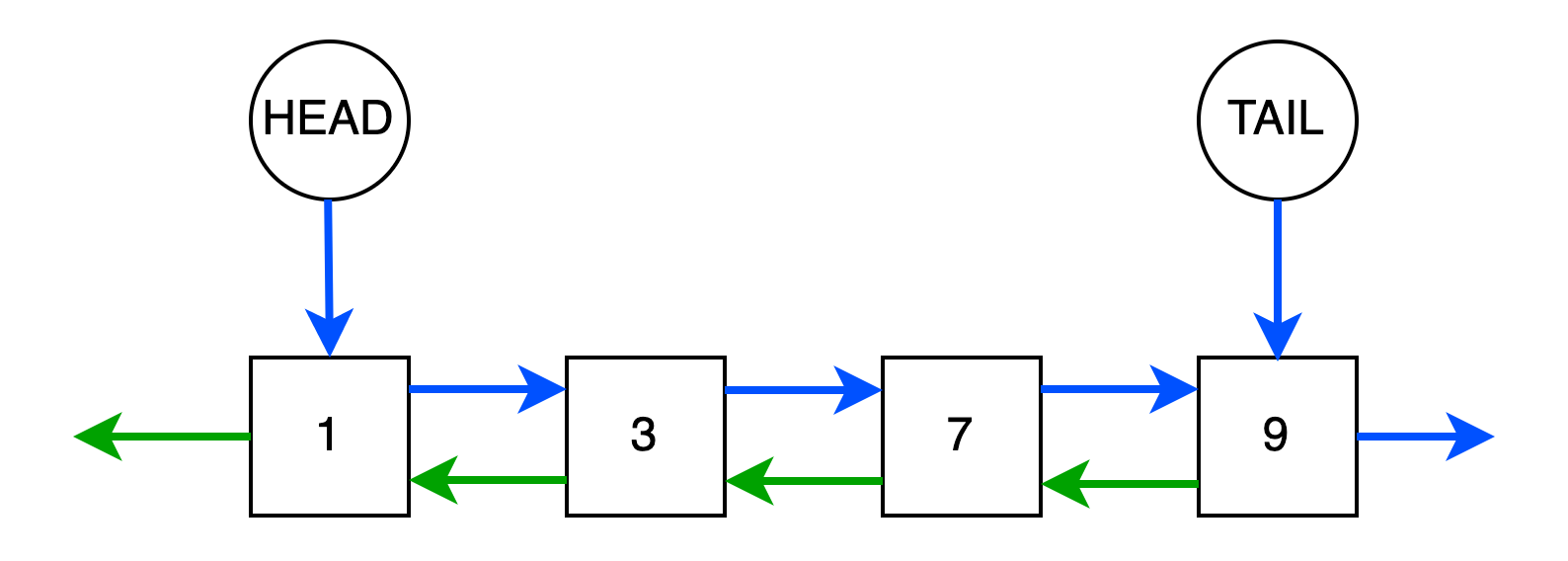
На рисунке выше синяя стрелка отображает связь на следующий элемент, а зеленая - на предыдущий. Как и в односвязном
списке, у структуры определены два указателя HEAD и TAIL на корневой head и конечный tail узлы
соответственно.
Каждый узел в двусвязном списке содержит не только значение, но и ссылку на следующий и предыдущий элемент. Программно его можно представить так:
@dataclass
class DoublyListNode:
"""
Узел двусвязного списка
"""
val: int
prev: Optional['DoublyListNode'] = None
next: Optional['DoublyListNode'] = None
Линейный поиск и доступ к элементу по индексу по двусвязному списку
Аналогично односвязному списку, в двусвязном мы также имеем:
- Мы не можем получить доступ к произвольному элементу за константное время.
- Для поиска значения в списке необходимо обойти все элементы начиная с головного.
- В худшем случае поиск элемента занимает линейное время O(n).
Вставка элемента в двусвязный список
Рассмотрим три вида вставки: вставка элемента в середину, в “голову” и в “хвост”.
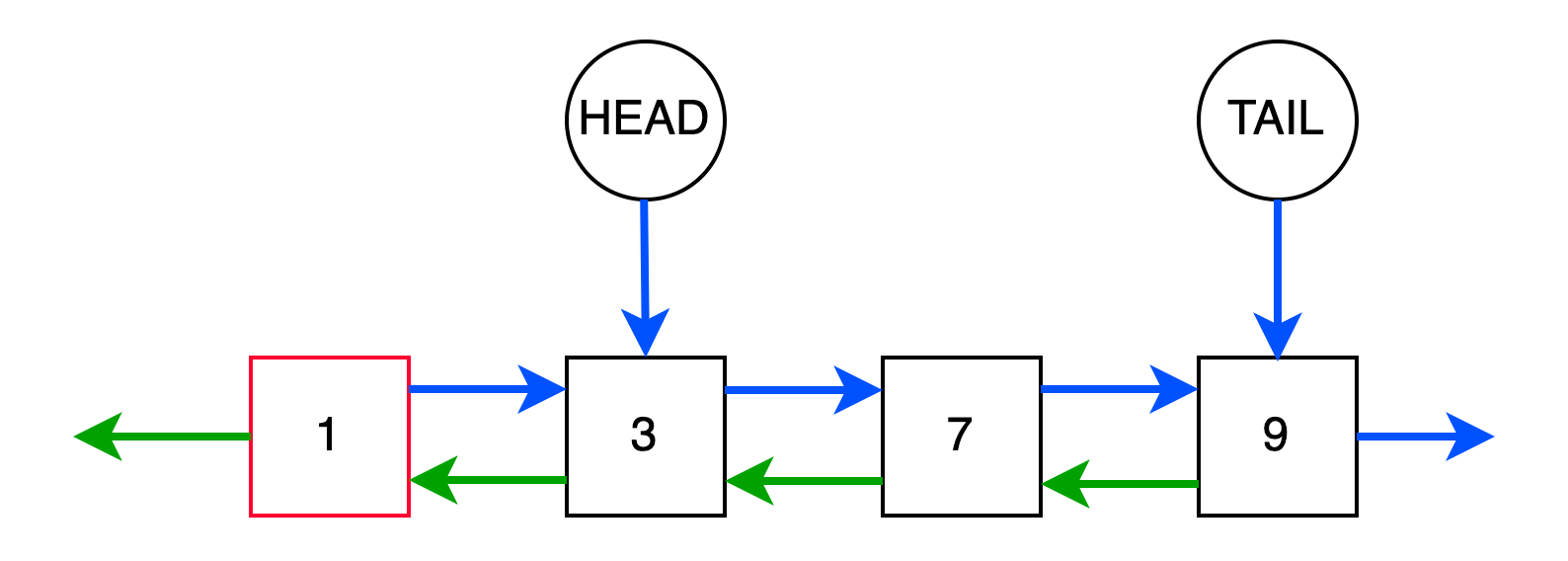
Вставка в начало изображена ниже. Алгоритм вставки следующий:
- Создаем узел
curи устанавливаемnextу него наhead - Если
headуже существует и список не пустой, то уheadустанавливаемprevнаcur - Если
tailне инициализирован (т.е. добавляемыйcurпервый в списке), то устанавливаемtailкакcur - Переназначаем
headнаcur
Вставку элемента в середину можно разделить на два шага:
- Связывания вставляемого элемента
curс узламиprevиnext - Удаление старых связей для
prevиnextи дальнейшее их переназначение наcur
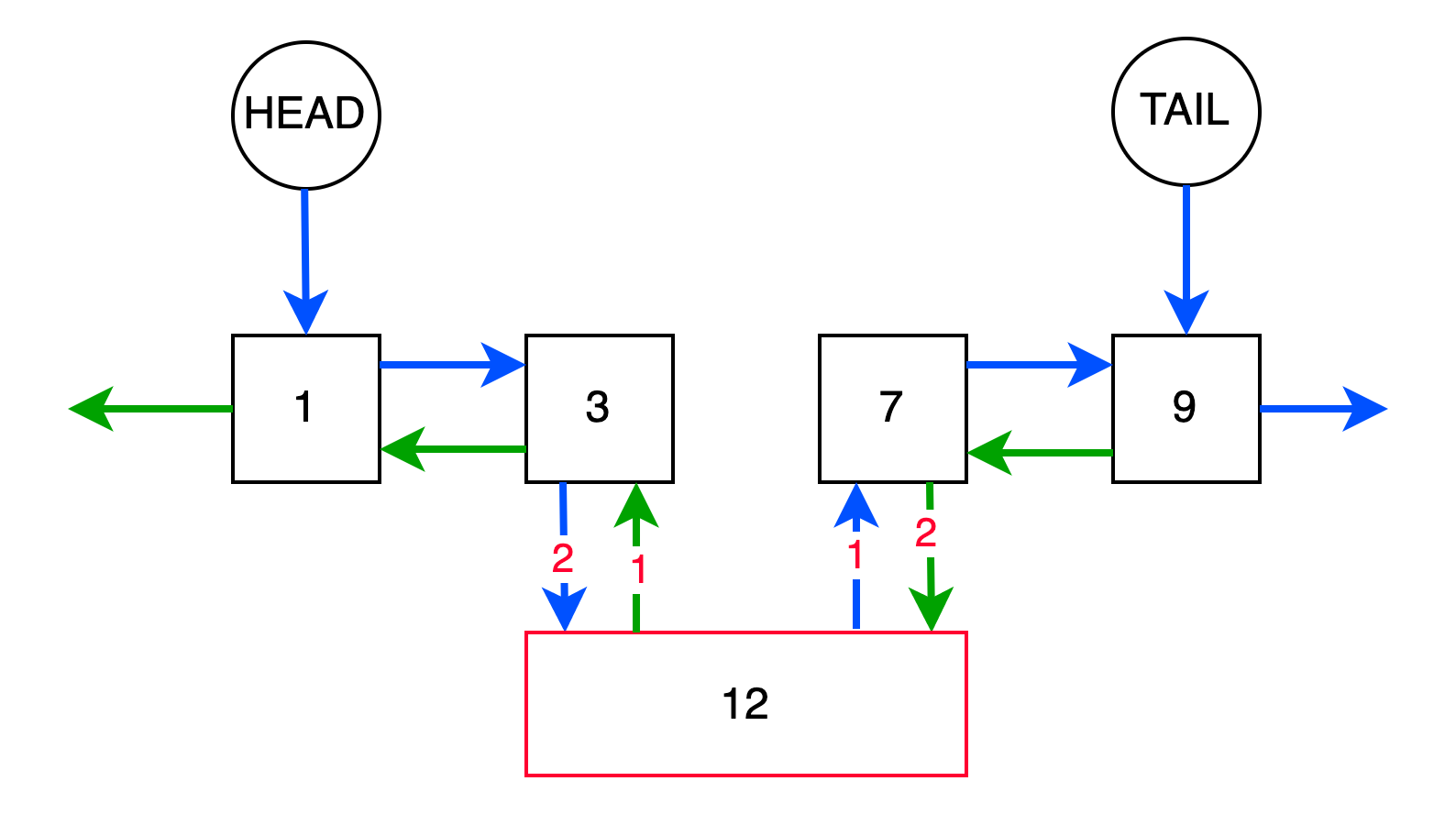
Операция займет O(1) вне зависимости от того какой узел следующий или предыдущий задается. В отличие от односвязного списка мы располагаем двумя связями. Следует заметить, что если происходит вставка по индексу, то изначально следует получить ссылку на правый или левый узел, а это займет O(n).
Вставка в хвост аналогична вставке в начало. Ее сложность оценивается в O(1).
Временная сложность операций:
Вставка элемента в середину - O(1). При условии, что задается узел для вставки, а не его индекс. Для вставки по индексу O(n).
Вставка элемента в “голову” - O(1).
Вставка элемента в “хвост” - O(1).
Операция удаления элемента
Алгоритм удаления из головы следующий:
- Берем голову
headи инициализируемcurзначением связиnext. - Если
curсуществует, удаляем у него значение связиprev. - Если
curне существует, в списке один элемент и мы его удаляем. Поэтому обнуляемtail. - Устанавливаем
headкакcur
Рассмотрим удаление из середины.
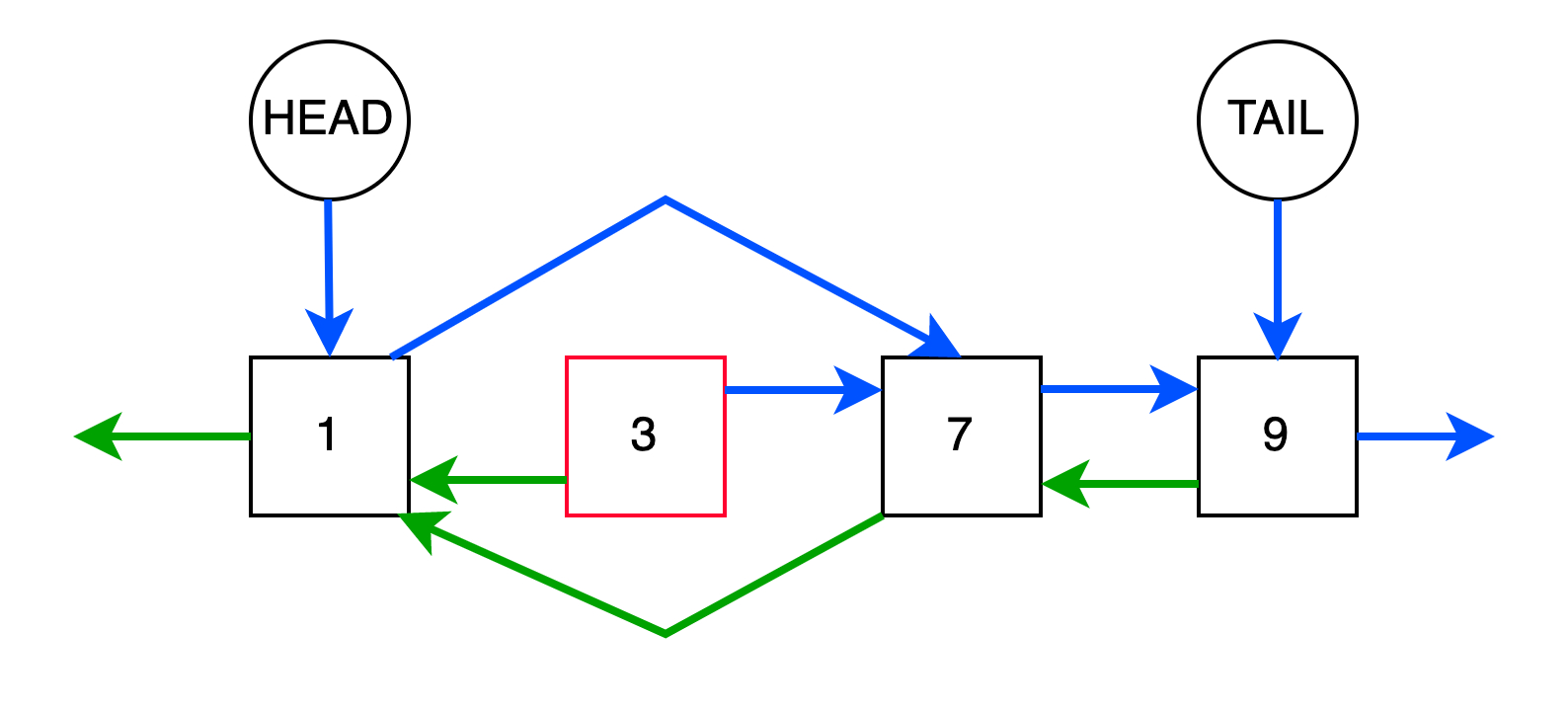
В отличие от односвязного списка, где эта операция занимает O(n) из-за того, что нам требуется найти предыдущий
элемент для создания связи, двусвязный список имеет ссылку на prev. Если мы хотим удалить существующий узел cur,
мы можем просто связать его предыдущий узел prev со следующим узлом next. Временная сложность O(1).
Удаление из конца списка аналогично удалению из головы, поэтому имеет временную сложность O(1).
Временная сложность операций:
Удаление элемента из “головы” - O(1).
Удаление элемента из середины - O(1). При условии, что задается узел для вставки, а не его индекс. Для удаления по индексу O(n).
Удаление элемента из “хвоста” - O(1).
Реализация двусвязного списка на языке python
"""
DoublyLinkedList
"""
from dataclasses import dataclass
from typing import Optional
@dataclass
class DoublyListNode:
"""
Узел двусвязного списка
"""
val: int
prev: Optional['DoublyListNode'] = None
next: Optional['DoublyListNode'] = None
class DoublyLinkedList:
"""
Реализация двусвязного списка
"""
def __init__(self):
self.head = None
self.tail = None
self.len = 0
def get(self, index: int) -> Optional[DoublyListNode]:
""" Получение узла по индексу """
cur = self.head
idx = 0
while idx != index:
if not cur:
return None
cur = cur.next
idx += 1
return cur
def add_at_head(self, val: int) -> DoublyListNode:
""" Добавление в голову """
cur = DoublyListNode(val)
cur.next = self.head
if self.head:
self.head.prev = cur
if not self.tail:
self.tail = cur
self.head = cur
self.len += 1
return cur
def add_at_tail(self, val: int) -> DoublyListNode:
""" Добавление в хвост """
cur = DoublyListNode(val)
cur.prev = self.tail
if self.tail:
self.tail.next = cur
if not self.head:
self.head = cur
self.tail = cur
self.len += 1
return cur
def add_at_index(self, index: int, val: int) -> Optional[DoublyListNode]:
""" Добавление по индексу """
if index > self.len:
return None
right = self.get(index)
if not right:
return self.add_at_tail(val)
left = right.prev
if not left:
return self.add_at_head(val)
cur = DoublyListNode(val)
cur.prev = left
cur.next = right
left.next = cur
right.prev = cur
self.len += 1
return cur
def delete_at_index(self, index: int) -> None:
""" Удаление по индексу """
curr = self.get(index)
if not curr:
return None
left = curr.prev
right = curr.next
if not left:
return self.delete_at_head()
if not right:
return self.delete_at_tail()
right.prev = left
left.next = right
self.len -= 1
return None
def delete_at_head(self) -> None:
""" Удаление из головы """
if not self.head:
return None
cur = self.head.next
if cur:
cur.prev = None
else:
# Если в списке один элемент и мы его удаляем
self.tail = None
self.head = cur
self.len -= 1
return None
def delete_at_tail(self) -> None:
""" Удаление с хвоста """
if not self.tail:
return None
cur = self.tail.prev
if cur:
cur.next = None
else:
# Если в списке один элемент и мы его удаляем
self.head = None
self.tail = cur
self.len -= 1
return None