data-structures-and-algorithms
Графы
Граф (graph, G) — это нелинейная структура данных, состоящая из множества элементов и связей между ними. Элементы называются вершинами графа и обозначаются V(vertices), а связи — ребрами, обозначаются как E (edges). Существует разные виды графов, рассмотрим несколько из них:
Ненаправленный граф - граф у которого ребра между вершинами не имеют определенного направления, т.е. из одной вершины в другую можно попасть как в прямом, так и в обратном направлении.
Направленный граф — это граф, у которого из одной вершины в другую можно попасть только одним способом, т.е. ребра имеют определенные направления.
Взвешенные графы отличаются тем, что их ребра имеют определенный вес, определяющий некоторую метрику перехода между соединяемыми вершинами.
Все виды графов изображены на рисунке ниже.
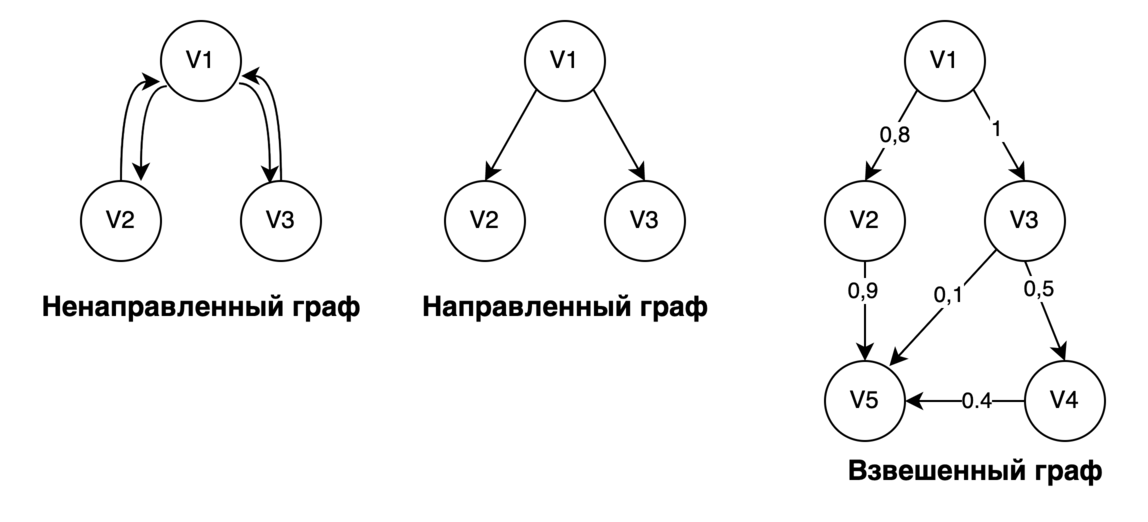
Помимо вершин и ребер граф определяется следующей терминологией:
Путь между вершинами описывает способ перехода из одной вершины в другую. Может существовать несколько путей для перехода. Например, для взвешенного графа существует три способа перехода из вершины V1 в V5: V1-V2-V5, V1-V3-V5, V1-V3-V4-V5.
Длина пути определяется количеством ребер в нем. Например, пути V1-V2-V5, V1-V3-V5, V1-V3-V4-V5 имеют длины 2, 2 и 3 соответственно.
Цикл - путь в графе, где начальная и конечная точка совпадают. Например, если рассматриваемый взвешенный граф был бы ненаправленным, то путь V1-V3-V5-V2-V1 являлся бы циклом.
Отрицательный вес цикла характерен только для взвешенного графа. Вес цикла — это сумма всех весов ребер цикла. Если это значение отрицательно, то можем говорить об отрицательном весе всего цикла.
Связность вершин. Если все вершины графа имеют между собой хотя бы один путь, то мы можем называть его связным. Напротив, вершины несвязного графа могут быть разделены по группам, которые называются компонентами связности.
Инцидентность – это когда вершина V является началом или концом ребра E.
Степень, или валентность вершины, графа — количество рёбер графа G, инцидентных вершине V. Данное определение применимо только для невзвешенных графов. Другими словами, валентность вершины, это количество ребер, которые соединяют данную вершину с другими вершинами. Для направленного графа, валентность вершины V1 равно двум.
Входящая и исходящая валентности вершин определены только для направленного графа. Входящая in-degree валентность вершины определяется количеством ребер, направленных в вершину. Исходящая out-degree валентность вершины определяется количеством ребер, направленных из вершины. Для рассматриваемого взвешенного, направленного графа in-degree валентность вершины V3 составляет 1, out-degree - 2.
Кратчайший путь - это один из всевозможных путей от одной вершины до другой с минимальным количеством ребер, т.е. с минимальной длиной.
Представление графов в памяти
Матрица смежности — один из способов представить граф в памяти компьютера. Номера строк и столбцов обозначают номера вершин, если вершина i связна с вершиной j, то в ячейке матрицы (i, j) записывается значение 1, в противном случае 0.
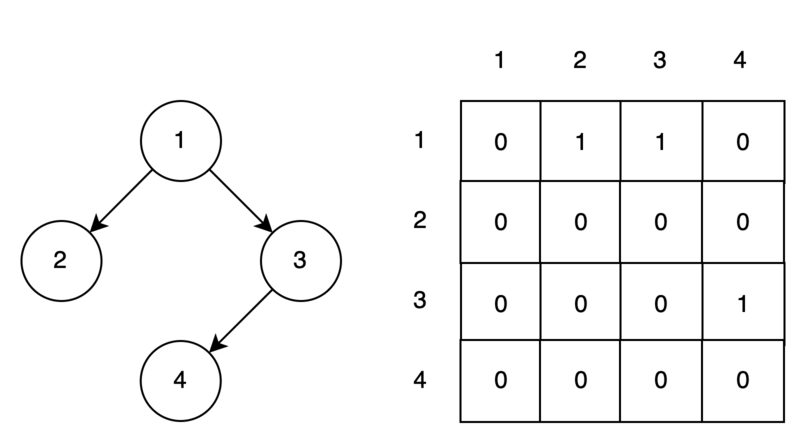
Список смежности содержит в себе информацию только о связанных вершинах. Как видим, он более экономный по памяти, чем матрица смежности.
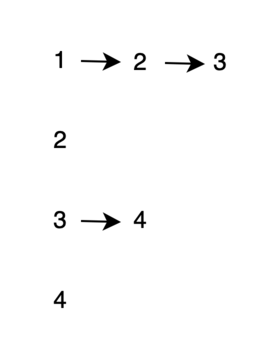
Список ребер - граф также можно представить в виде списка значений вида [(1,2), (1,3), (3,4)]. Элементы массива представляют собой ребра графа. В ненаправленном графе порядок вершин не важен, в направленном важен.
Матрицу и список смежности, а также список ребер можно реализовать на основе простого массива.