data-structures-and-algorithms

Куча

Куча - это полное бинарное дерево, обладающее следующими свойствами:

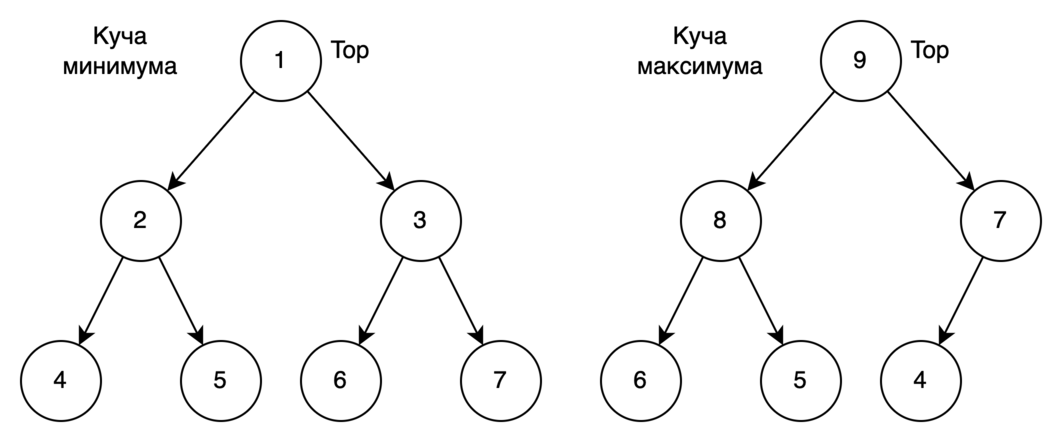
1. Для кучи минимумов каждый узел в куче имеет значение, не превышающее значений его дочерних узлов. Следовательно, верхний элемент (корневой узел) имеет наименьшее значение в куче. Для кучи максимумов каждый узел в куче имеет значение, не меньше значений его дочерних узлов. Следовательно, верхний элемент (корневой узел) имеет наибольшее значение в куче.
2. Все уровни кучи, кроме, возможно, последнего, полностью заполнены, а все узлы последнего уровня максимально левые. Таким образом заполнение производится по уровням слева направо.

Ниже представлены два вида кучи: кучи минимума и максимума.

Операции просеивания

Операции просеивания используются после вставки и удаления элемента для того, чтобы выполнялось основное свойство кучи о ключах(п.1). Различают просеивание вверх и просеивание вниз. Рассмотрим каждый алгоритм более детально. Далее будем рассматривать кучу минимума.

Вставка элемента

Просеивание вверх - это всплытие добавленного листа дерева до тех пор, пока не будет выполнено условие, что новый узел в куче имеет значение большее значения родителя и не превышающее значений его дочерних узлов. Таким образом мы меняем просеиваемый узел с родителем до тех пор, пока он не станет корнем или пока его значение меньше значение родителя.

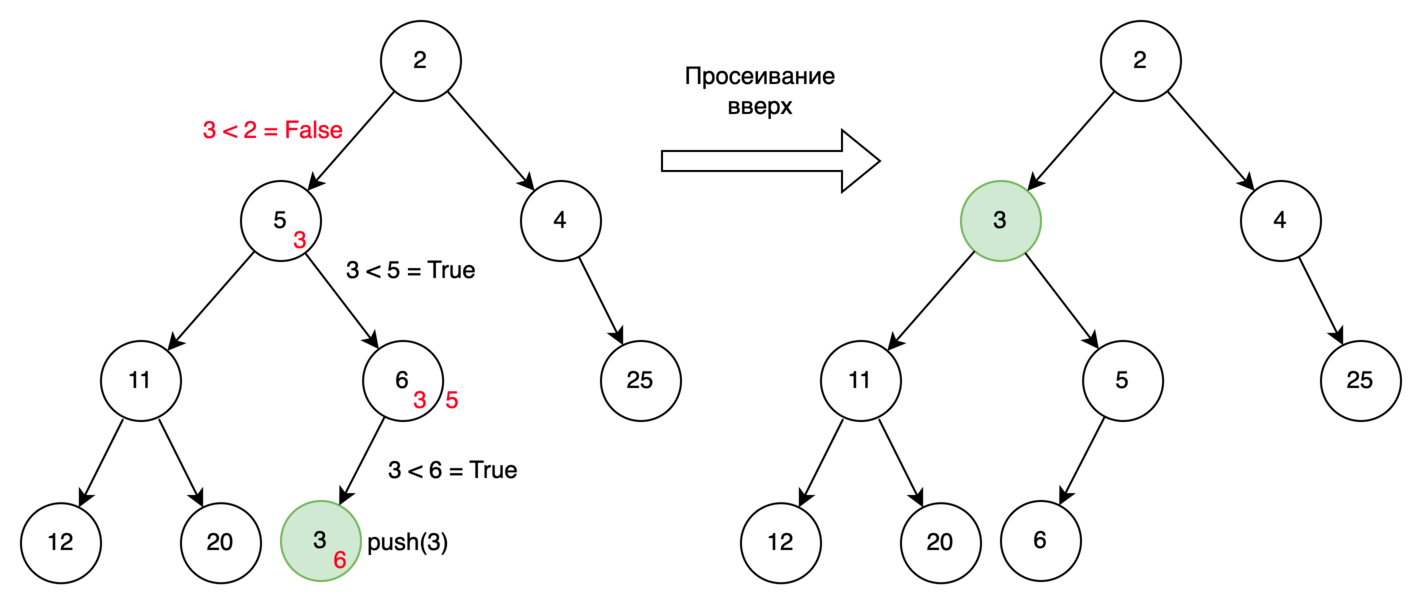
Сложность данной операции O(logN).

Удаление элемента

Просеивание вниз - это погружение самого верхнего элемента, пока он не будет удовлетворять основному свойству кучи о ключах. Алгоритм следующий:

1. Берем самый правый в последнем ряду элемент и переносим его на место удаляемого элемента, т.е. на вершину кучи. Определяем элемент как просеиваемый.
2. Если у просеиваемого элемента два сына, определяем среди них того, у которого меньший ключ. Меняем этот узел с просеиваемым если нужно.
3. Если у просеиваемого элемента один сын, меняем этот узел с просеиваемым если нужно.
4. Если после перестановки у просеиваемого элемента нет сыновей, то завершаем алгоритм, свойство кучи восстановлено.

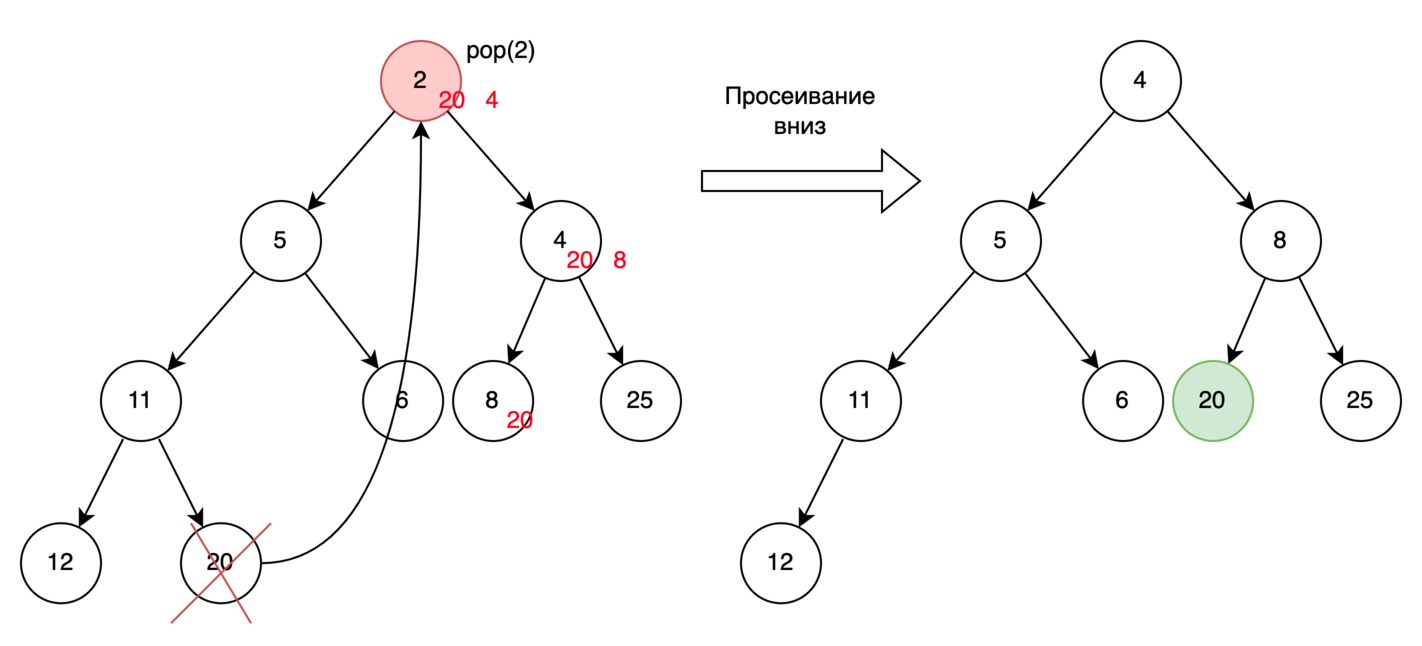
Сложность данной операции O(logN).

Определение минимального или максимального элемента

Свойство ключей кучи гарантирует, что на ее вершине будет всегда находиться минимальный или максимальный элемент. Поэтому эта операция очень простая и состоит в чтении с вершины кучи.

Сложность данной операции O(1).

Реализация кучи в памяти

Для реализации кучи очень удобно использовать массив. Для этого мы нумеруем узлы кучи подряд по слоям слева направо, и в таком порядке располагаем их в обычном массиве.

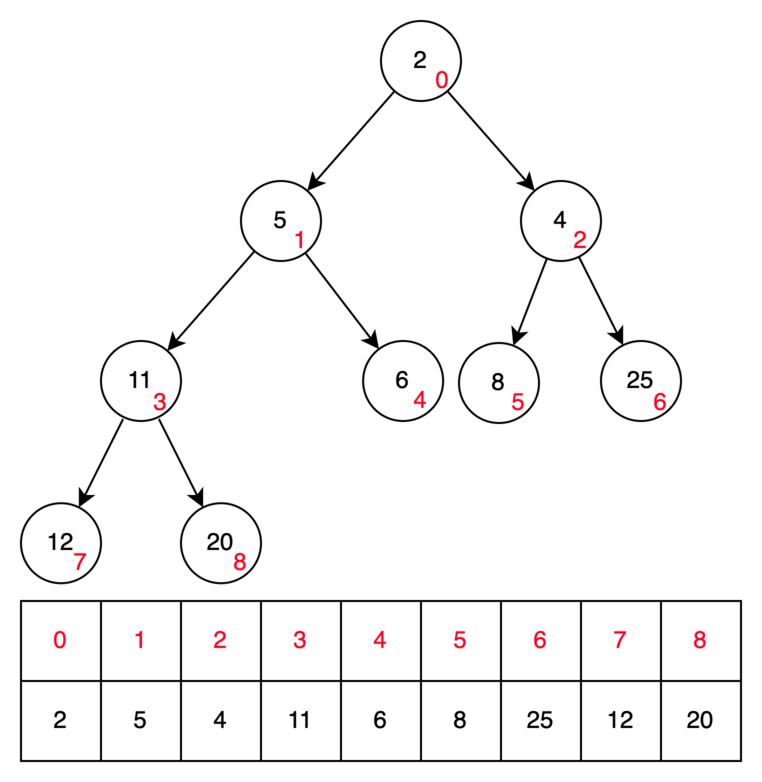
Тогда индексы хранения левого и правого ребенка для i-ого элемента будут 2 * i + 1 и 2 * i + 2 соответственно. Индекс родителя вычисляется по формуле (i - 1 ) // 2. Ниже представлена реализация кучи минимума на python. Представление в виде массива значительно сокращает использование памяти по сравнению с классической реализацией бинарных деревьев в виде объектов и ссылок на них.

class MinHeap:
    """ Реализация кучи минимумов на python с использованием массива """

    def __init__(self):
        self.heap_list = []

    def is_empty(self):
        return not bool(self.heap_list)

    def push(self, key: int):
        """ Добавление в кучу """
        self.heap_list.append(key)
        cur_idx = len(self.heap_list) - 1
        while cur_idx > 0 and self.heap_list[cur_idx] < self._get_parent(cur_idx):
            parent_idx = _get_parent_index(cur_idx)
            # Меняем текущий элемент с родителем
            self.heap_list[cur_idx], self.heap_list[parent_idx] = self.heap_list[parent_idx], self.heap_list[cur_idx]
            cur_idx = parent_idx

    def peek(self):
        """ Получение минимума """
        if len(self.heap_list) > 0:
            return self.heap_list[0]

        return None

    def pop(self):
        """ Извлечение с вершины кучи """
        if len(self.heap_list) == 1:
            return self.heap_list.pop()

        result = self.peek()
        # Берем самый правый в последнем ряду элемент и переносим его на место удаляемого элемента
        self.heap_list[0] = self.heap_list.pop()
        cur_idx = 0

        while True:
            max_idx = len(self.heap_list) - 1

            left_idx = _get_left_child_index(cur_idx)
            right_idx = _get_right_child_index(cur_idx)

            if left_idx > max_idx and right_idx > max_idx:
                #  Если после перестановки у просеиваемого элемента нет сыновей, то завершаем алгоритм
                break

            if left_idx <= max_idx and right_idx <= max_idx:
                # Если у просеиваемого элемента два сына
                max_child_idx = left_idx if self.heap_list[left_idx] < self.heap_list[right_idx] else right_idx
            elif left_idx <= max_idx:
                max_child_idx = left_idx
            else:
                max_child_idx = right_idx

            if self.heap_list[max_child_idx] < self.heap_list[cur_idx]:
                self.heap_list[cur_idx], self.heap_list[max_child_idx] = self.heap_list[max_child_idx], self.heap_list[
                    cur_idx]
                cur_idx = max_child_idx
            else:
                break

        return result

    def _get_parent(self, idx: int) -> int:
        """ Получение родительского ключа """
        parent_idx = _get_parent_index(idx)
        return self.heap_list[parent_idx]

    def __str__(self):
        return str(self.heap_list)


class MaxHeap:
    """ Реализация кучи максимума на python с использованием массива """

    def __init__(self):
        self.heap_list = []

    def is_empty(self):
        return not bool(self.heap_list)

    def push(self, key: int):
        """ Добавление в кучу """
        self.heap_list.append(key)
        cur_idx = len(self.heap_list) - 1
        while cur_idx > 0 and self.heap_list[cur_idx] > self._get_parent(cur_idx):
            parent_idx = _get_parent_index(cur_idx)
            # Меняем текущий элемент с родителем
            self.heap_list[cur_idx], self.heap_list[parent_idx] = self.heap_list[parent_idx], self.heap_list[cur_idx]
            cur_idx = parent_idx

    def peek(self):
        """ Получение минимума """
        if len(self.heap_list) > 0:
            return self.heap_list[0]

        return None

    def pop(self):
        """ Извлечение с вершины кучи """
        if len(self.heap_list) == 1:
            return self.heap_list.pop()

        result = self.peek()
        # Берем самый правый в последнем ряду элемент и переносим его на место удаляемого элемента
        self.heap_list[0] = self.heap_list.pop()
        cur_idx = 0

        while True:
            max_idx = len(self.heap_list) - 1

            left_idx = _get_left_child_index(cur_idx)
            right_idx = _get_right_child_index(cur_idx)

            if left_idx > max_idx and right_idx > max_idx:
                #  Если после перестановки у просеиваемого элемента нет сыновей, то завершаем алгоритм
                break

            if left_idx <= max_idx and right_idx <= max_idx:
                # Если у просеиваемого элемента два сына
                max_child_idx = left_idx if self.heap_list[left_idx] > self.heap_list[right_idx] else right_idx
            elif left_idx <= max_idx:
                max_child_idx = left_idx
            else:
                max_child_idx = right_idx

            if self.heap_list[max_child_idx] > self.heap_list[cur_idx]:
                self.heap_list[cur_idx], self.heap_list[max_child_idx] = self.heap_list[max_child_idx], self.heap_list[
                    cur_idx]
                cur_idx = max_child_idx
            else:
                break

        return result

    def _get_parent(self, idx: int) -> int:
        """ Получение родительского ключа """
        parent_idx = _get_parent_index(idx)
        return self.heap_list[parent_idx]

    def __str__(self):
        return str(self.heap_list)


def _get_parent_index(i: int) -> int:
    """ Индекс родителя """
    return (i - 1) // 2


def _get_left_child_index(i: int) -> int:
    """ Индекс левого ребенка """
    return 2 * i + 1


def _get_right_child_index(i: int) -> int:
    """ Индекс правого ребенка """
    return 2 * i + 2

This site is open source. Improve this page.