data-structures-and-algorithms

Связанные списки

Связанный список - это линейная структуры данных, элементы в которой хранят ссылки на следующие объекты списка и располагаются в разных фрагментах памяти. Различают односвязные и двусвязные списки.

Односвязный список

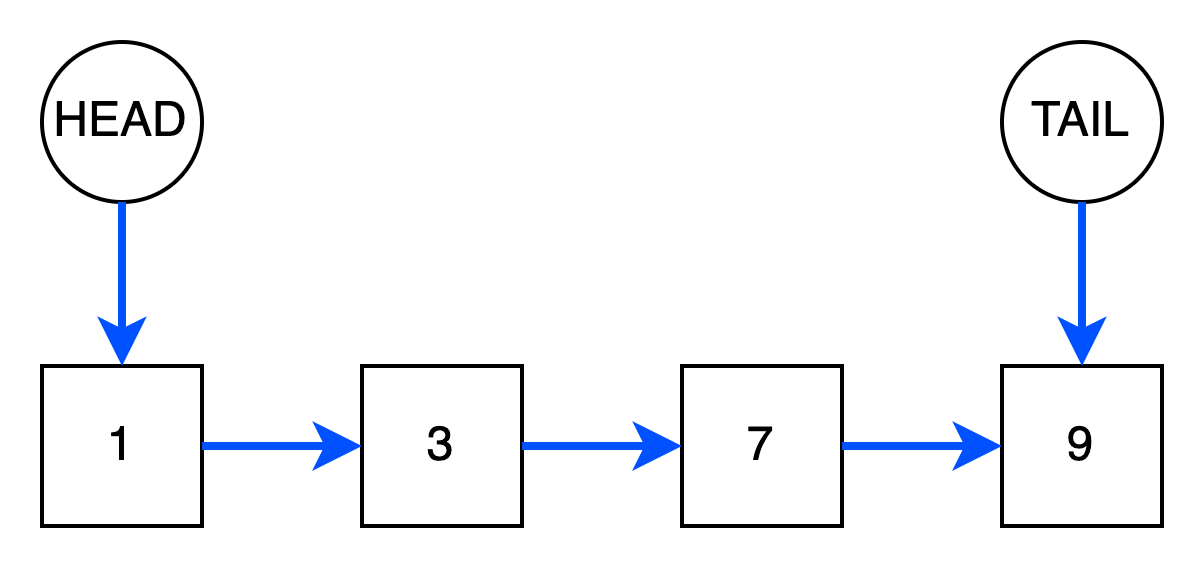
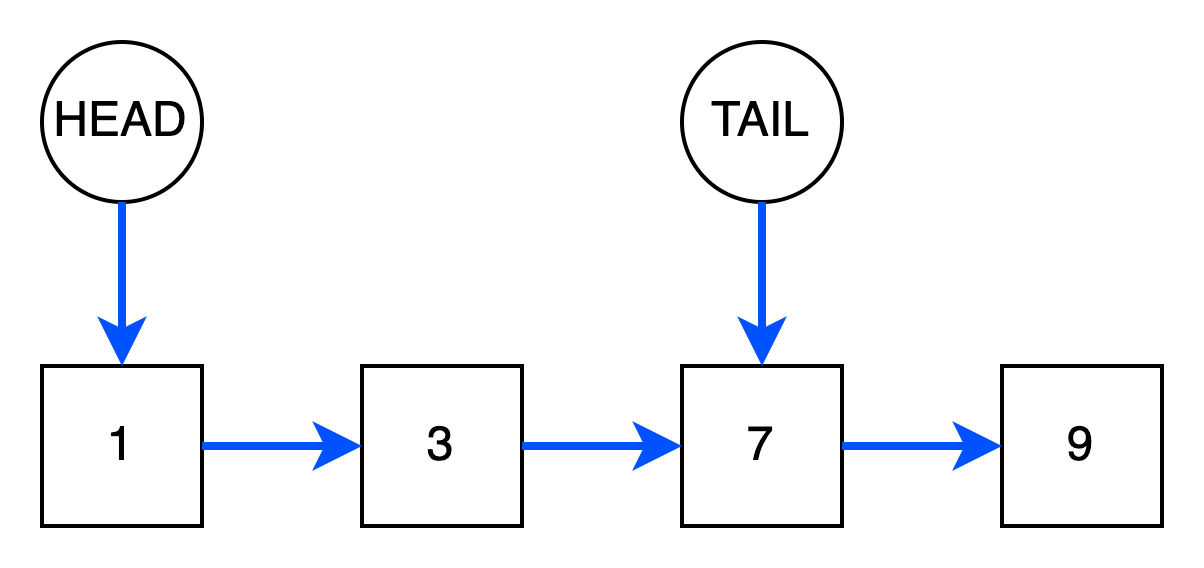
На рисунке выше синяя стрелка отображает связь на следующий элемент. HEAD и TAIL - указатели, хранящие ссылки на головной и конечный узлы.

Каждый узел в односвязном списке содержит не только значение, но и ссылку на следующий элемент. Программно его можно представить так:

class SinglyListNode:
    """
    Узел односвязного списка
    """
    def __init__(self, value, next_node):
        self.value = value
        self.next_node = next_node

Т.о. односвязный список можно однозначно определить головным указателем HEAD. Заметим, что рассматриваемый список имеет два указателя HEAD и TAIL на корневой head и конечный tail узлы соответственно. Если обращаться к концу списка нам не нужно(например, удалять из конца списка), то указатель TAIL можем не хранить.

Линейный поиск по односвязному списку

Линейный поиск по односвязному списку, как и по массиву, выполняется за линейное время. Чтобы найти заданное значение, следует перебрать все элементы списка, начиная с головы, используя связи. Сложность данной операции оценивается в O(n).

Доступ к элементу по индексу и присвоение значения по индексу

В отличие от массива, используя односвязный список, мы не можем получить доступ к элементу по индексу за константное время. Чтобы получить i-ый элемент, мы должны пройтись по всем связям с первого узла до i-ого. Это имеет временную сложность O(n). Операция присвоения по индексу имеет аналогичную временную сложность.

Вставка элемента в односвязный список

Чтобы вставить элемент в середину после заданного узла prev, необходимо:

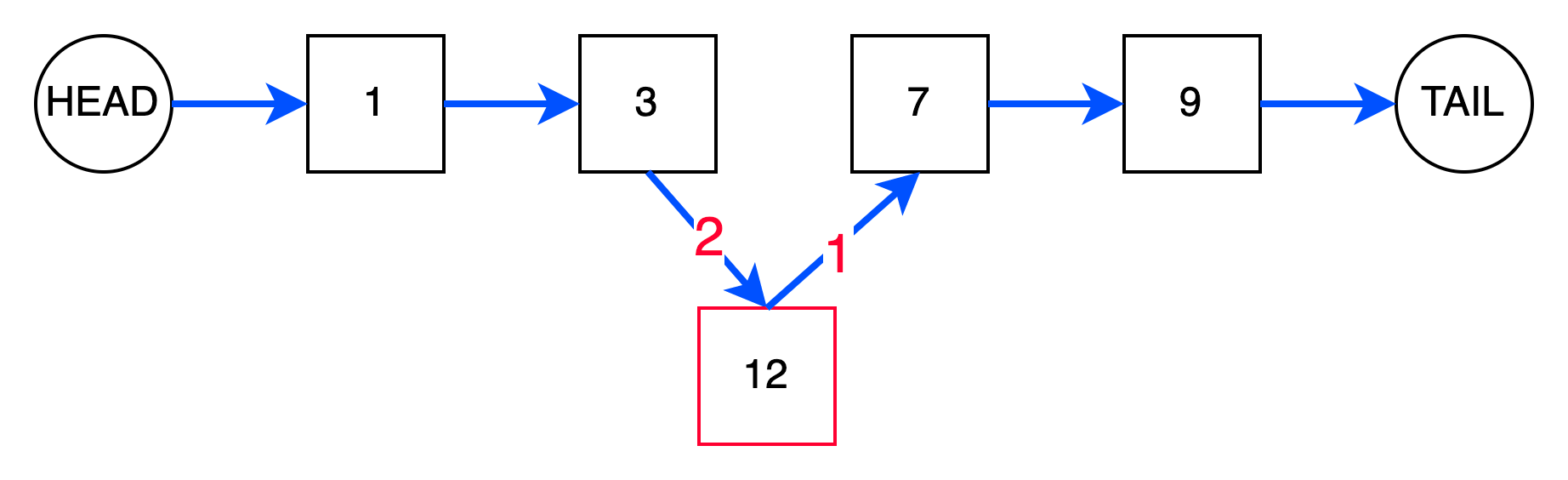
1. Инициализировать новый узел cur с заданным значением.
2. Связать cur с узлом next, который следует после prev.
3. Связать prev с узлом cur.

В отличие от массива, мы не должны сдвигать все элементы в право для вставки. Мы просто инициализируем новый элемент и переопределяем связи. Эта операция очень эффективна и имеет константную сложность O(1). Заметим, что если для вставки в середину задается следующий элемент next, то для нахождения prev следует выполнить линейный поиск, который занимает O(n).

Чтобы вставить элемент в начало списка необходимо:

1. Инициализировать новый узел cur с заданным значением.
2. Связать cur с узлом head, который в настоящий момент является головным.
3. Переназначить головной узел на cur

Операция добавления в голову также занимает константное время.

Наконец последняя операция вставки - вставка в конец. Алгоритм данной операции следующий:

1. По указателю TAIL мы понимаем конечный элемент tail.
2. Далее инициализируем новый узел cur с заданным значением.
3. Связываем конечный элемент tail с новым узлом cur.
4. Переназначаем указатель TAIL на новый элемент cur.

Операция добавления в хвост оценивается как O(1). Заметим, что если список не хранит указатель TAIL на последний элемент, то операция займет O(n), т.к. пришлось бы сначала найти последний элемент.

Временная сложность операций:

Вставка элемента в середину - O(1). При условии, что задается предыдущий элемент prev, после которого следует выполнить вставку.

Вставка элемента в “голову” - O(1)

Вставка элемента в “хвост” - O(1). При условии, что список хранит указатель TAIL на последний элемент, иначе
O(n).

Удаление элемента из односвязного списка

В данном случае удаление из середины займет линейное время. Порядок действий будет следующий:

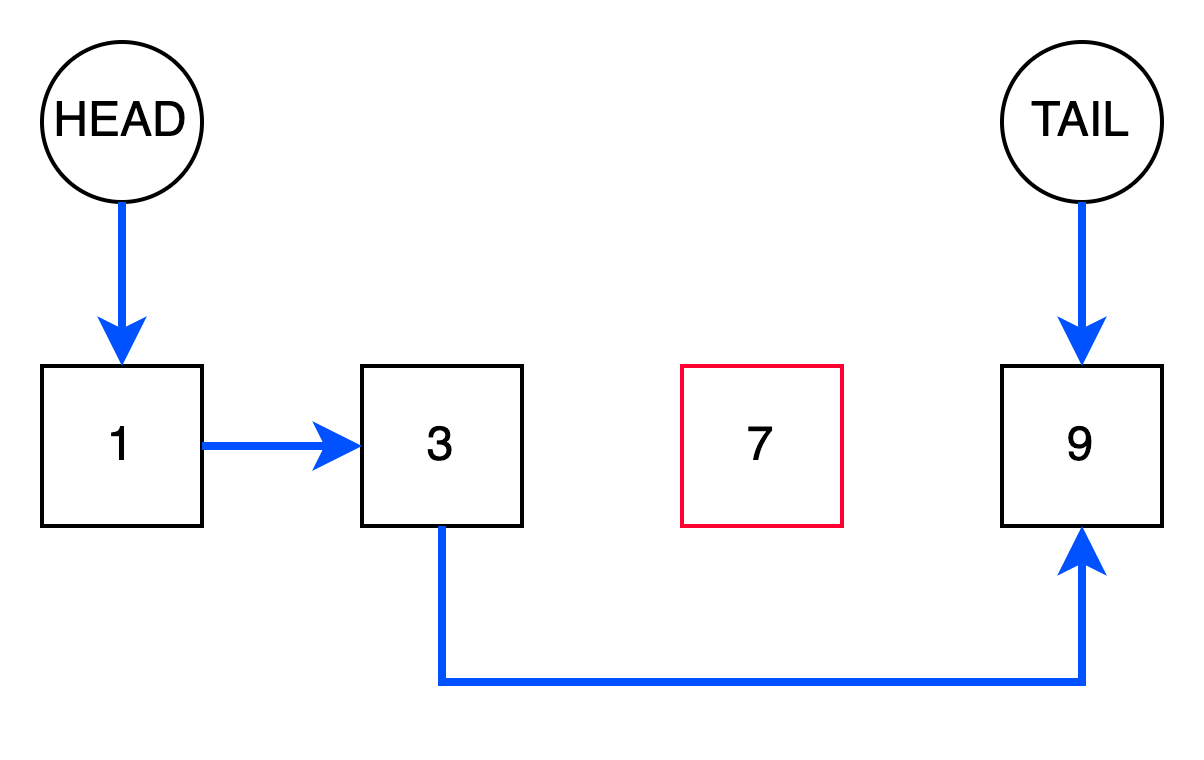
1. Поиск предыдущего prev и следующего next элементов. Если на следующий элемент мы имеем ссылку и его поиск занимает константное время, то для нахождения предыдущего элемента потребуется выполнить линейный поиск начиная с головного узла.
2. Выполнить связывание предыдущего prev и следующего next элементов.

Т.к. операция поиска предыдущего prev элемента занимает линейное время, то и общая сложность операции оценивается как O(n).

Как упоминалось ранее, указатель HEAD определяет головной узел и, следовательно, весь список. Удаление элемента из “головы” означает, что надо просто переназначить указатель HEAD на следующий next элемент.

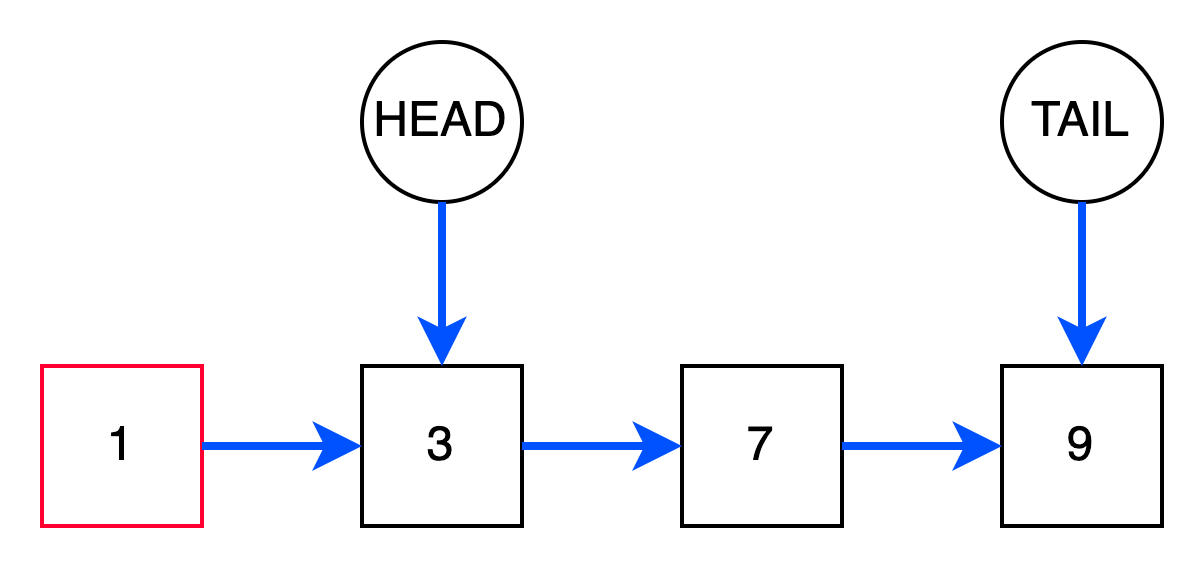
Операция удаления элемента из “головы” оценивается как O(1) и является очень эффективной.

При удалении элемента из “хвоста” нам следует переместить указатель TAIL на элемент, который предшествует конечному узлу.

Однако для определения предыдущего prev узла нам нужно выполнить линейный поиск начиная с головы, т.к. ссылки на предыдущие узлы в односвязном списке не хранятся. Операция поиска записает линейное время, а следовательно общая оценка сложности удаления из хвоста - O(n).

Временная сложность операций:

Удаление элемента из “головы” - O(1)

Удаление элемента из середины - O(n)

Удаление элемента из “хвоста” - O(n)

This site is open source. Improve this page.